High-threshold and low-overhead fault-tolerant quantum memory - Bivariate Bicycle Codes
二 07 五月 2024

随着量子计算的产业逐年扩大，量子硬件不断规模化，量子比特数上升到1000量级。在此规模的NISQ硬件上，能否实现有效的量子算法？能否通过编码出高质量的逻辑比特来提升计算能力？能否更高效的编码出数量更多的逻辑比特？

针对这些问题，IBM团队提出了基于qLDPC码的高编码率编码方案，例如可以用144个物理比特编码出12个逻辑比特，四月发表在Nature上。 本文是qLDPC第一篇登上Nature的理论文章，且以数值计算为主，反应了基于qLDPC码的高编码率量子纠错码对实现容错量子计算的重要性。 本期将对这篇文章进行图文解读，学习qLDPC的整体脉络和前沿进展。

(Bravyi et al, Nature 2014)

研究背景：为什么需要qLDPC码？

为了量子系统中的噪声，量子芯片需要尽可能与外界环境相互隔离。而实现量子计算需要对量子比特进行操控，因此需要将量子芯片与所处环境进行耦合，从而不可避免的引入了噪声。 物理噪声的累积阻碍了大规模量子算法的实现。量子纠错提供了一个解决方案，将k个逻辑比特编码在更多数量的n个物理比特上，以此来将噪声降低到可以接受的范围。只要物理噪声低于某个容错阈值，量子纠错就是有效的。这个容错阈值依赖于量子纠错码的选择、症状测量线路和解码算法。

本文提出了一个端到端的量子纠错协议，基于一类LDPC码实现了容错内存。本方法的线路噪声模型的容错阈值达到了0.7%，与在容错性能上领先了20年的表面码相当。

量子纠错码在数学上，可以定义成希尔伯特空间的一个子空间。不同的子空间对应了不用的纠错码。最常见的选取子空间的方式使稳定子生成法(Stabilizer formalism)，即先定义测量算符，由所有测量算符构成了本征值全为+1的本征态空间就是用来存储逻辑信息的子空间。量子纠错码比较重要的参数包括\([[n,k,d]],w,p_{th}\)，分别是物理比特数、逻辑比特数、距离、测量权重、容错阈值。其中，距离与纠错能力正相关，低的测量权重和高的容错阈值对实验友好，逻辑比特数与物理比特数的比值\(k/n\)为编码率，编码率越高，资源利用率越高。另外，测量算符是否是近邻的，与实验难度和硬件要求息息相关，也因此引出了目前的两大类纠错码。一类是基于近邻算符的拓扑码，包括表面码。近邻算符的代价是受限的距离和趋向于零的编码率。 另一类属于qLDPC码(quantum low-density parity check code 量子低密度奇偶验证码)，没有近邻要求，但要求低测量权重，也就是说，其测量矩阵是稀疏的随机矩阵。qLDPC码已经可以实现线性的编码率和线性的距离。

表面码的理论已经相对完善，已经有多个基于表面码的量子计算体系架构，从物理比特的硬件实现一直到应用算法的编译。qLDPC码要实现高编码率，也必须在体系架构的每个层面给出解决方案,相关进展参考下表。

@Weilei Zeng 2024

(Bravyi et al, Nature 2014) 给出了离实用性最近的一次方案，为目前NISQ芯片的容错方案提供了参考。本文的核心贡献包括

  • 给出了几百比特规模的显性构造方式，权重是6
  • 高编码率，高距离
  • 给出了测量线路
  • 给出了解码器，并拓展到线路模型，和距离计算
  • 模拟出高容错阈值
  • 给出了平面layout

技术背景：

希尔伯特空间的任意子空间都可以被定义成一个量子纠错码。为了缩小好的纠错码的搜索空间，往往在构造方式上增加各种限制，同时得到理想的性质。两种常见的构造方式就是乘积和循环。

张量乘可以将一维空间上升到二维以及更高维度，从而将乘积系统中的测量、解码和逻辑算符等分解为低维度的操作。比如Hypergraph product codes, homological product codes, subsystem product codes, lifted product codes, etc. 因为张量乘定义具有对称性，此处我们规定A是行，B是列。在测量矩阵中，A的每一行是一个测量算符，作用在量子比特阵列的每一行上。B的每一行也是一个测量算符，作用在量子比特阵列的每一列上。

img

lattice \(A\otimes B\)

循环测量矩阵的优势是使其测量算符为一定范围内的近邻算符，如图所示，每一行代表一个测量，不管系统所大，都只需要同时测量相距不超过4的比特。相对于随机矩阵来说，环状矩阵不要求任意两个位置的物理比特的连接，可适用于有低拓展性的硬件架构。

循环矩阵有几种描述方式。除了直接写出整个矩阵，我们可以借助单位矩阵I和平移矩阵S，以下是大小为7的平移矩阵。

S作用在任意向量上，将使向量平移一个单位，并且最后一位回到第一位。S^T则会反向平移，如下图所示。其中箭头端点和顶点所在位置组成了一个向量。

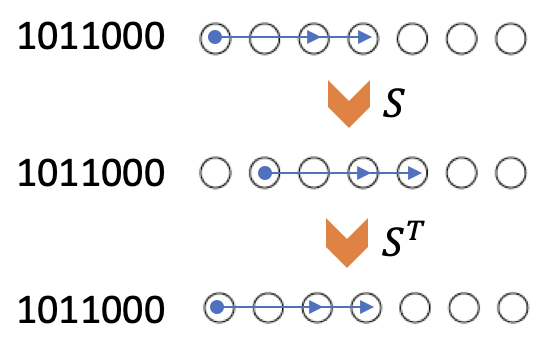
现在H可以用S的多项式来表示 \(H = I + S^2 + S^3\)。

其中，\(S^2\)代表将单位矩阵平移两个单位，\(S^3\)代表将单位矩阵平移三个单位，相加后得到了以\(1011000\)为生成元的循环矩阵

因为H是一个循环矩阵，S作用在H上，在允许行变换的情况下，会得到H本身。

借助乘积和循环的概念，就可以构造出具有准近邻算符的qLDPC码，如下图所示。左侧基于重复码测量矩阵构造，也就是常见的表面码。右侧基于权重为3的循环矩阵构造，测量算符权重为6，最远两比特门距离不超过4，逻辑比特数为18，远高于表面码的2逻辑比特。图中也给出了相应BB码的框架中的多项式。

@Kovalev and Pryadko 2013 http://www.faculty.ucr.edu/~leonid/

Bivariate Bicycle码的构造

本文中Bivariate Bicycle (BB)码的构造用到了以下二维平移矩阵

$$x = S_l \otimes I_m, y = I_l \otimes S_m $$

单位矩阵I“不起作用”，当平移矩阵S位于前面时，代表了在行方向进行平移；当平移矩阵S位于后面时，代表了在列方向进行平移。l m决定了二维阵列的大小是\(m \times l\)。因此x的作用是向右平移，y向下。翻过来，\(x^T\)向左，\(y^T\)向上。

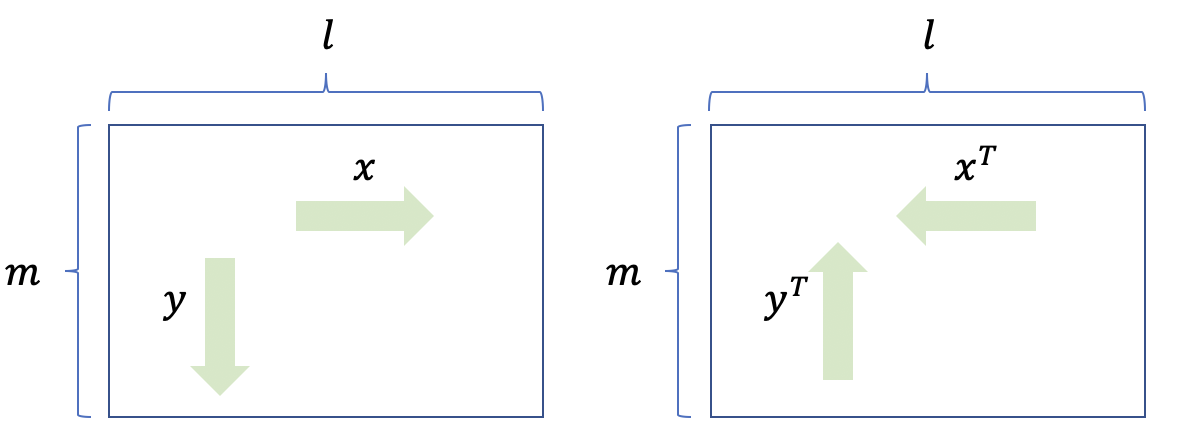
基于这几个基本元素的多项式，我们可以构建二维向量，（也可以认为是矩阵）。BB码的构建是基于两个项数为3的矩阵多项式。

$$A = A_1 + A_2 + A_3, B=B_1 + B_2 + B_3$$

其中\(A_i,B_j\)是x或y的幂。

那么BB码定义为

$$H^X=(A|B),H^Z=(B^T|A^T)$$

因为循环矩阵的特性，可以验证这两个测量矩阵\(H^X(H^Z)^T = 0\) mod 2, 是合格的CSS码的定义条件。Lemma 1给出了其参数，\(n=2lm, k=2\times dim(ker(A) \cap ker(B))\)。逻辑比特数k可以直接由矩阵A和B确定。

接下来以\([[144,12,12]]\)码为例图解其构造方式，其多项式为

$$A = x^3 + y + y^2, B = y^3 + x + x^2, l=12,m=6$$

在二维阵列中用下图表示,测量比特位于箭头顶点。

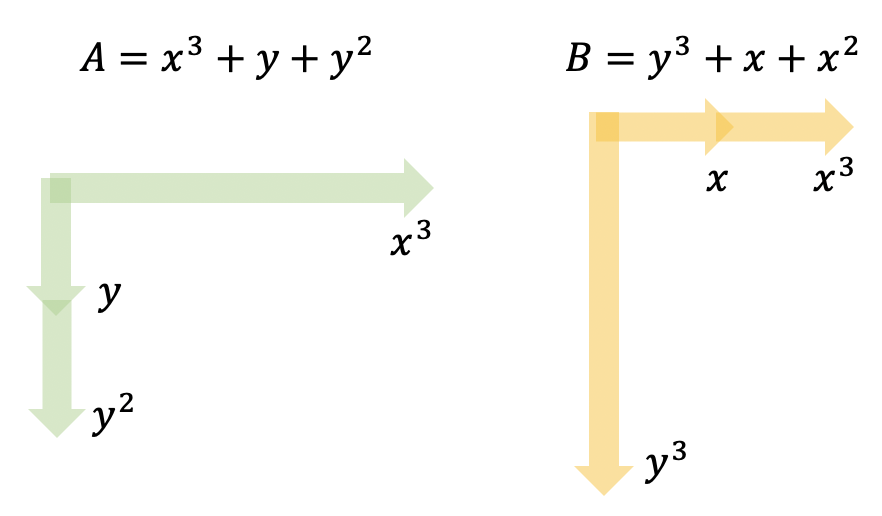
BB码将所有物理比特划分为四个区块的叠加，分别标记为L,R,X,Z，每一个区块都是\(m \times l\)的矩形阵列。

上图的矩阵多项式A所测量的比特位于L区块，B位于R区块。这是因为A位于测量矩阵H的左边（left）。A和B中的物理比特的相对位置并不唯一。作者为了实现其中四个比特的近邻测量，将A、B以下图中的相对位置进行组合。

(Bravyi et al, Nature 2014)

类似的，可以用下图来描述\(A^T,B^T\)

可以看出来，\(A,B,A^T,B^T\)的相对位置可以以图中的菱形为基准来确定。菱形的较远的顶点代表了需要长距离连接的比特位置，近处顶点代表了X和Z测量的辅助比特的位置。这样每个菱形就对应了唯一的X测量和Z测量，以及对应辅助比特的位置。通过对菱形进行平移可以得到新的测量算符。这样选择的好处是X和Z类型的测量算符中都有四个近邻比特，且用于测量的辅助比特位于其正中。在下文的物理比特布局部分，作者基于这个布局在两个平行二维阵列上实现了没有交叉的测量线路。事实上，并没有足够证据说明这个选择一定是最优的，比如可以选择让A中的两个近邻比特与B中的远比特相邻，也是一个可选的方案。

借用这两个多项式和图中的基准菱形用于定位，已经完整的定义了\([[144,12,12]]\)码。

现在回顾一下Bivariate Bicycle Codes的定义和命名。 Bicycle是因为H由左侧 的A和右侧的B两个循环矩阵构成。Bivariate代表定义循环矩阵用到了两个变量x和y，对应了两个方向的平移。因此将这个码命名为双变量自行车码。

Pininterest img @Image by Pinterest

本文除了144码，一共测试了6种码，它们由不同的大小或者不同的多项式。

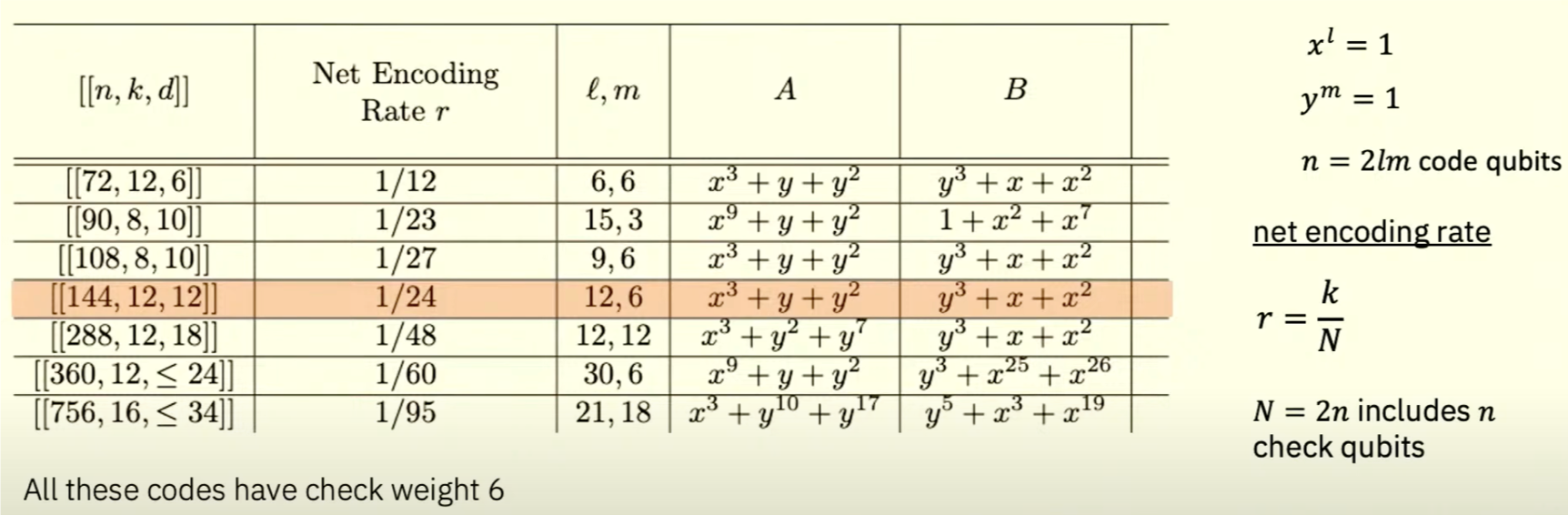
@Slides by Ted Yodar 2024

Syndrome Circuit 测量线路

本文中的BB码的测量权重全部为6.其测量可以由一个辅助比特和6个CNOT门来实现，如下图所示。

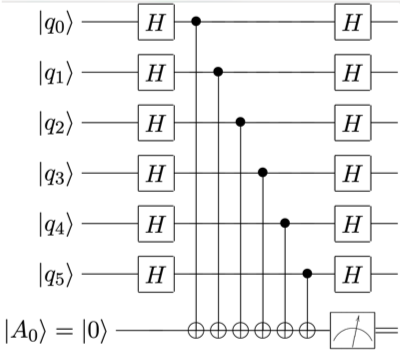
@Weilei Zeng 2024

平均下来，在每一轮测量中，每个数据比特和辅助比特上都会作用6个CNOT门。通过恰当的对CNOT门进行排序，可以是整个电路更加紧凑，耗时最少，积累的噪声也更少。作者用程序搜索了936中排序方式，选择了下图中深度为7的线路。其线路距离\(d\leq 10\)

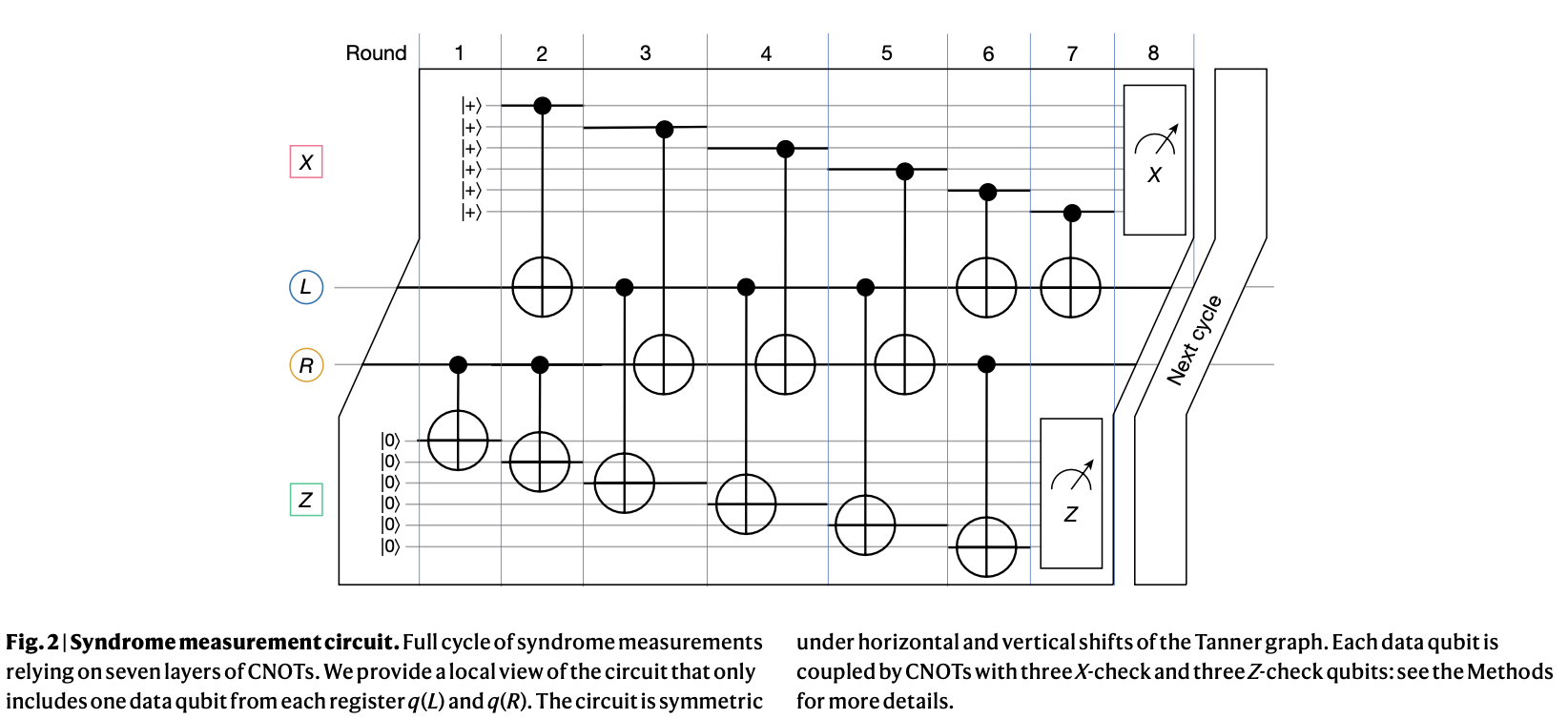@Fig. 2 (Bravyi et al, Nature 2014)

Decoding: BP+OSD

BB码的解码由Belief Propagation + OSD完成。BP是经典纠错码的最优解码算法，但在量子纠错码中受限于其解码图中的短环，已经有数十种方案用来克服短环的问题，目前从解码复杂度和纠错能力来说，最好的是BP+OSD。本文进一步的将BP+OSD应用在线路噪声模型上。先用预设的噪声模型训练出BP解码器中的比特-测量图的权重系数。再用此解码器对每一个测量的症状进行解码。

本文进一步给出了用BP计算纠错码的距离的上界的方法和用BP计算给定线路的距离的上界的算法。解码和计算距离是两个形式上类似的问题，一般认为其理论上是等价的两个问题。例如random window decoder既可以用来解码，也可以用来计算距离[5]。但这两者的等价性目前还没有文章给出直接的证明或结论，是一个可以探究的问题。

数值模拟结果

基于以上BB码的构建，测量线路，和解码器，可以进行蒙特卡洛模拟得到容错阈值。

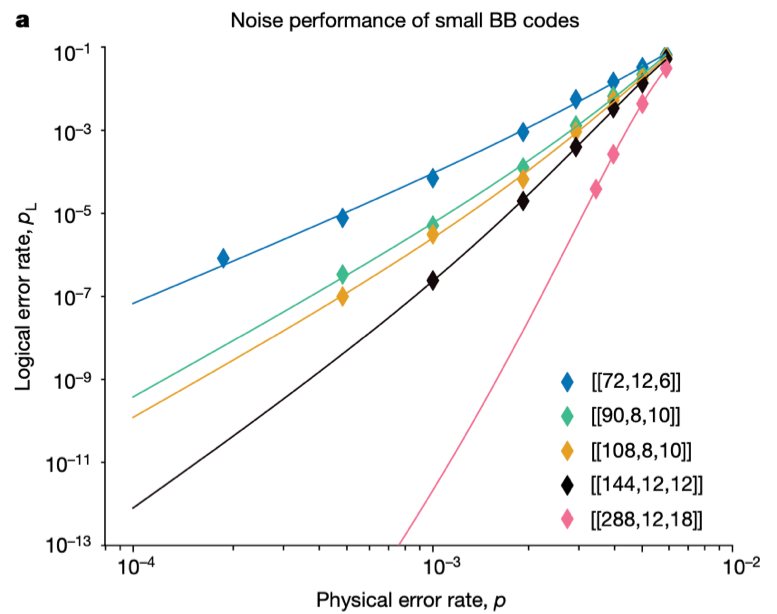
(Bravyi et al, Nature 2014)

几个关键数值在下表中列出，包括准阈值（逻辑噪声与物理噪声相等的点，也叫break-even point），以及当物理噪声为0.001和0.0001是的逻辑噪声。

(Bravyi et al, Nature 2014)

通过与表面码进行比较，为了实现12个逻辑比特，BB码消耗了144个物理比特，而表面码在同等逻辑噪声的情况下，消耗的物理比特介于1452和2028之间。BB码的资源消耗降低了一个数量级。

(Bravyi et al, Nature 2014)

BiPlanar Layout 双平面布局

BB码的核心假设和主要挑战之一是位于基准菱形上的长程双比特门，目前不存在于任何已知的量子计算硬件平台上。为了实现基于平面图的测量，即所有双比特门没有交叉，作者提出了基于两个平面的布局。原来每个权重是6的测量包括三个L区块的物理比特（A的行权重是3）和三个R区块的物理比特（B的行权重是3）。现在以L+L+R和L+R+R的形式把所有物理比特分割到两个平面上，两个平面上测量参考以下测量矩阵。

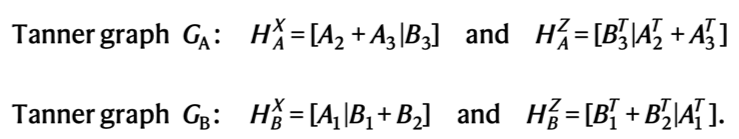
这样每个平面上的测量都可以用一个没有交叉的平面图里来表示。

(Bravyi et al, Nature 2014)

这里有一个疑问，就是这两个平面图上的辅助比特对应同一个测量。那么怎么结合这两个辅助比特的测量结果得到原来的的权重是6的测量呢？或者只有一个辅助比特，存在于某一个平面上？这点文章作者并没有解释。因此这里假设是前者，讨论其实现方案。

一般的，稳定子测量通过相应的物理比特与辅助比特的双比特门以及辅助比特上的测量门来实现。实际上，这里不要求是一个辅助比特，也可以是多个辅助比特，如下图所示。可以通过辅助比特间的双比特门将辅助比特上的测量互相传递。

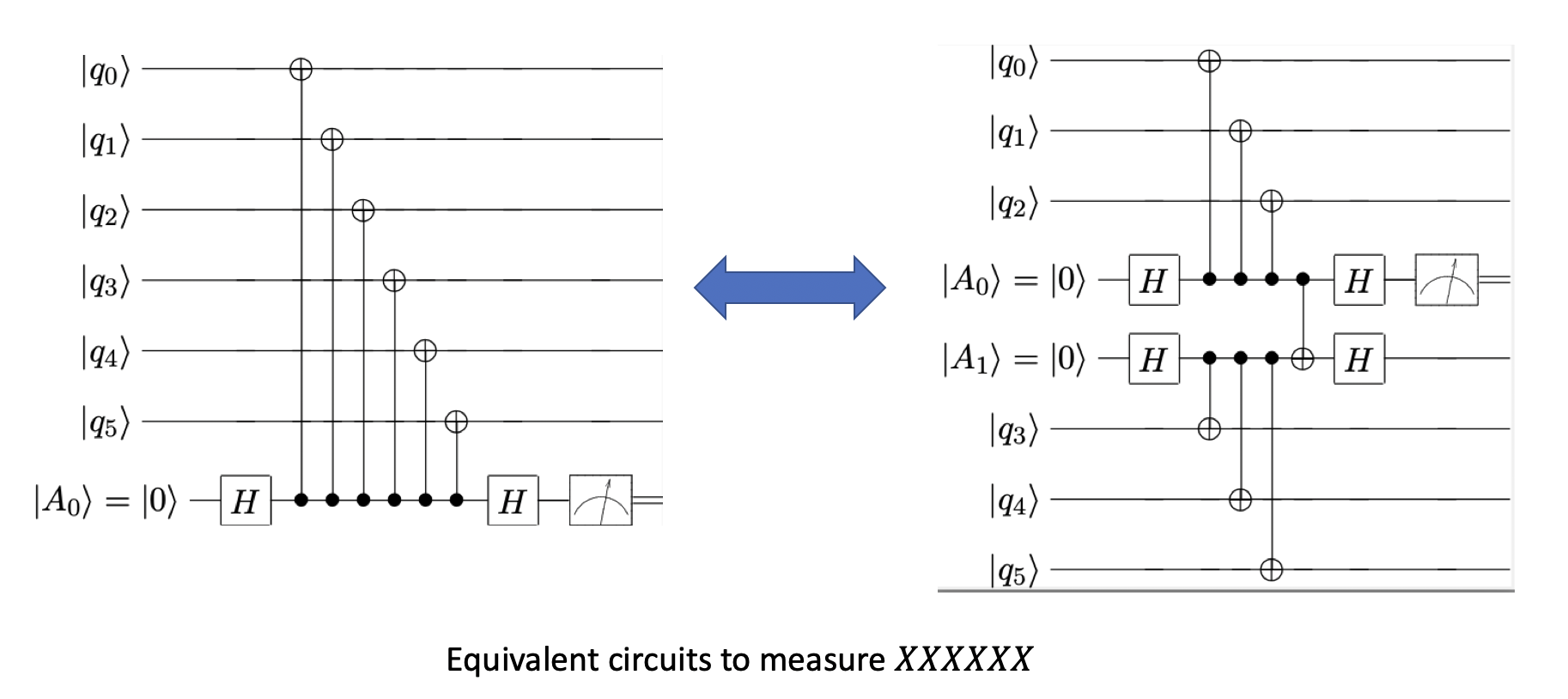
@Weilei Zeng 2024

借用此方法，BB码的两个平面的对应位置各有一个辅助比特，并可以进行双比特门操作。因此辅助比特比单平面的情况下会多出一倍，同时这并不是两个相互独立的物理比特二维平面阵列，而是在所有辅助比特的位置都要求双比特门连接。尽管其是近邻连接，也对硬件实验提出了不小的要求。

至此，BB码确实在两个平面上实现了测量。但本布局最大的问题，是BB码的构造是基于周期性边界条件。也就是说，不管是一个平面，还是两个平面，这些平面其实都是torus（甜甜圈）。如何将torus改为具有边界的矩形阵列是一个巨大挑战？一般将周期性边界切割以后，会影响边界上相应稳定子的互易性和纠错码的参数性质，包括编码率、距离、测量权重等。

延伸课题

基于本文的成果和进展，提出若干开放性问题

  • 除了文中的权重是6的例子，是否考虑项目为4的多项式，权重为8？权重为8的测量算符理论上也可以在双平面布局中实现。
  • 如何去掉周期性边界条件？一般对平面进行切割时，边界上的测量算符的互易性会破坏，这将如何影响纠错码的编码率和距离等参数以及纠错表现？
  • 解码算法。众所周知，BP解码算法离最优解码算法还有很大的提升空间。
  • 在多少物理比特的系统上，qLDPC码会超越表面码的资源利用率和纠错表现？本文给出了144物理比特的例子，(Xu et al 2024)给出了1000比特量级的例子。在100比特以内，也就是目前的实验水平上，能否构造出高质量的qLDPC码？
  • 适配硬件平台：本文纠错码的构造是基于超导，在拓展到离子阱、中性原子和光量子平台时有何优劣？
  • 高维度的架构是否能提升参数和容错能力。借助time-space code或者冗余测量，二维纠错码实际处于四维空间中。BB码的架构在高维度如何推广？

Acronym 缩写

  • ancilla qubit 辅助比特
  • quantum error-correctin code 量子纠错码
  • qLDPC, quantum low-density parity check code 量子低密度奇偶验证码
  • syndrome 症状
  • distance 距离
  • circuit noise model 线路噪声模型
  • stabilizer 稳定子
  • check/measurement 测量（算符）

References

Category: research Tagged: qLDPC bicycle codes QEC Published by Weilei Zeng

Page 1 of 1